發電機定子繞組

  1. Home
  2. Knowledge / Generator Knowledge (TW)
  3. 同步發電機概述與結構原理
  4. 發電機定子繞組

線圈定義

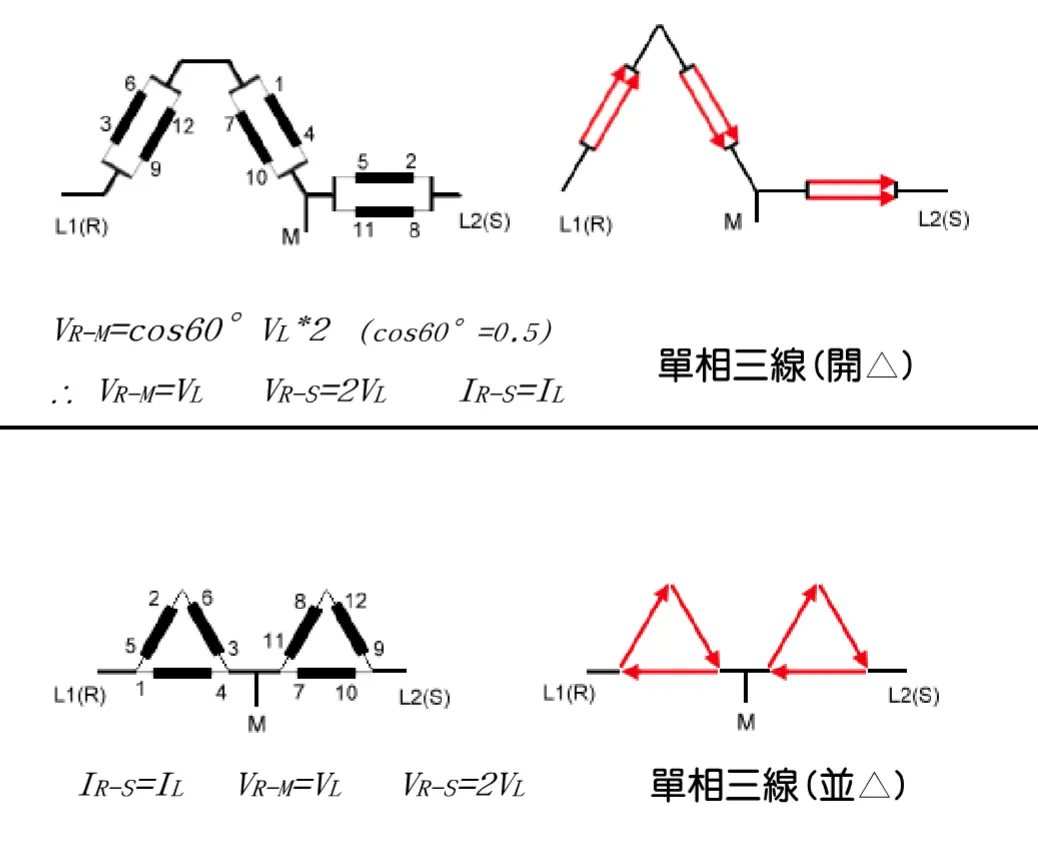
線圈定義

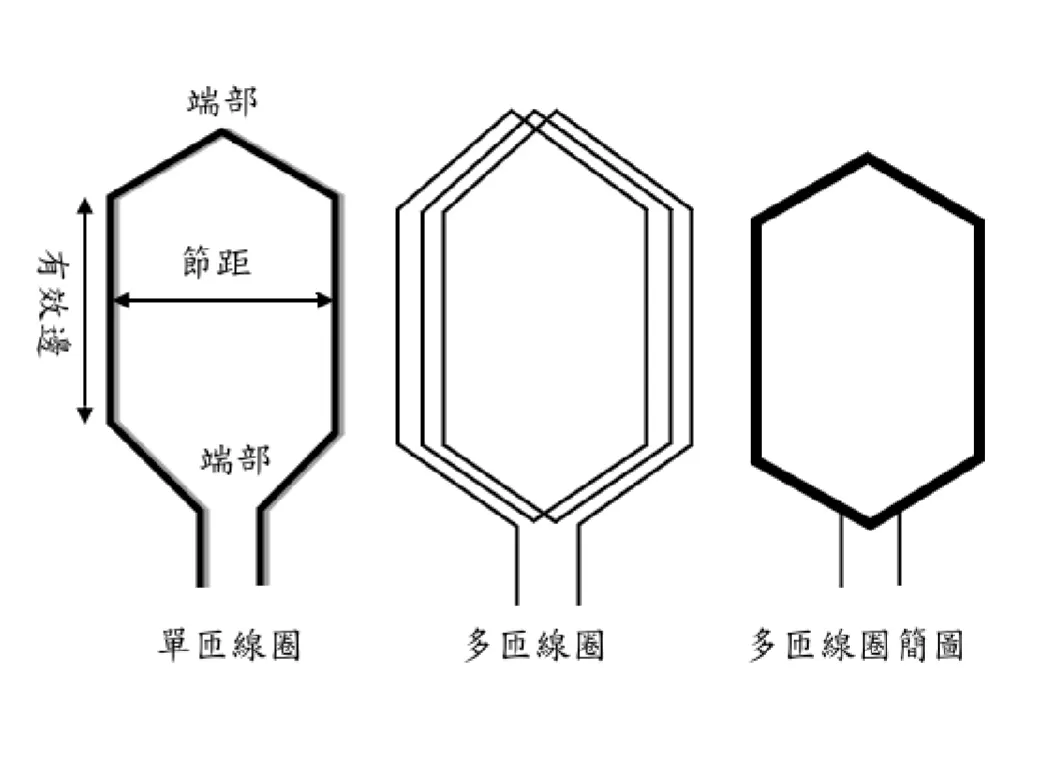
繞組概念

繞組概念
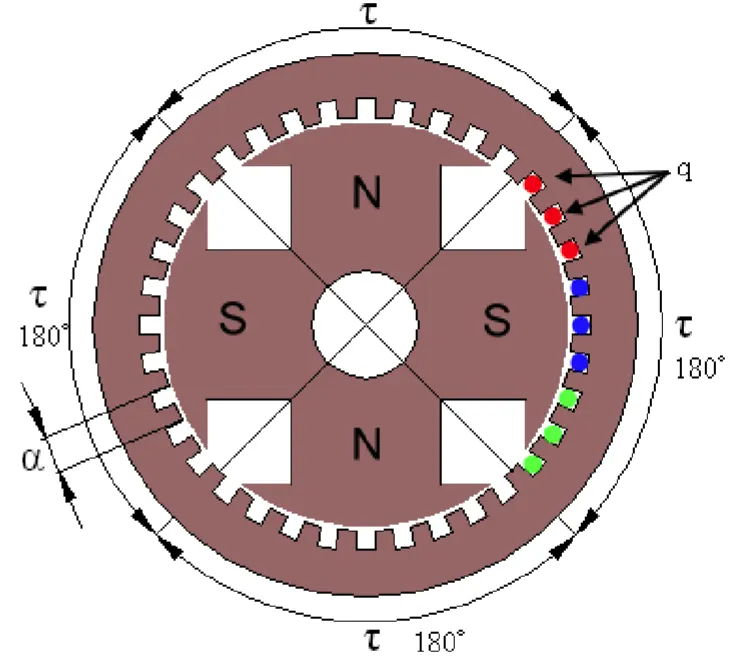
  • 極距 τ \tau ：沿定子鐵心內圓每個轉子磁極所占的定子槽數( τ \tau =36/4=9)
  • 槽距角 α \alpha ：一個定子槽所占的電角度數稱為槽距角( α \alpha =180/9=20°)
  • 每極每相槽數q：每個極距內每相所占的槽數稱為每極每相槽數(q=9/3=3)

導線感應電壓

導線感應電壓
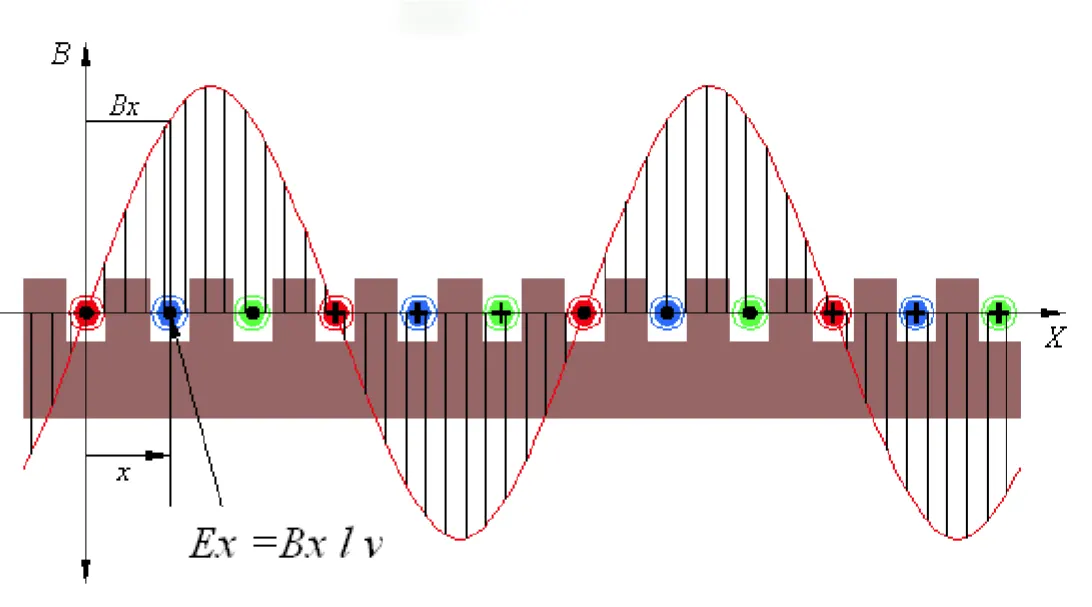
  • E x Ex ：在 x x 角度時導線的感應電壓
  • B x Bx ：在角度 x x 時通過導線的磁通量
  • l l ：導線在定子槽內的有效長度(有效邊)
  • ν \nu ：勵磁場(轉子)旋轉速度

導體中的感應電勢

  • 感應電勢的波形
    e x ( t ) = B x l ν e_x(t) = B_xl\nu
    感應電勢隨時間變化的波形和磁感應強度在空間的分佈波形相一致。
    只考慮磁場基波時，感應電勢為正弦波。
  • 感應電勢的頻率
    磁場轉過一對極(p)，導體中的感應電勢變化一個週期；
    轉速為n (r/min)的電機，每秒鐘轉過(pn/60)對極；
    導體中感應電勢的頻率f=(pn/60)Hz
  • 感應電勢的大小
    感應電勢的最大值： E n m a x = B δ l ν E_{nmax} = B{_\delta}{l\nu}
    導體與磁場的相對速度： v = 2 p τ n / 60 v = 2p{\tau}n/60
    感應電勢的有效值： E n = E n m a x 2 = 2.22 f ϕ 1 E_n = \cfrac{E_{nmax}}{\sqrt{2}} = 2.22f{\phi}_1
小結：繞組中均勻分佈著許多導體，這些導體中的感應電勢有效值，頻率，波形均相同；但是他們的相位不相同。

集中繞組

集中繞組

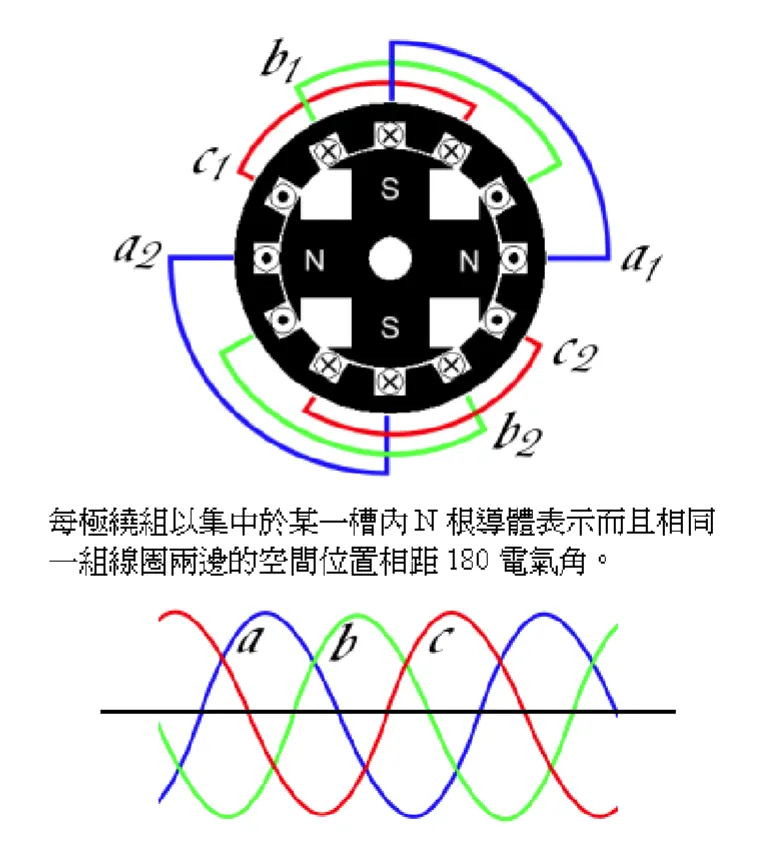
典型的集中繞組是轉子一對極內只有三個定子齒、槽，定子槽數Q與極對數p的關係為Q/p=3，三個齒上套三個線圈，分別屬於a、b、c三相，多對極的電機，具有p組線圈，可以將它們串聯或並聯構成三相繞組。

集中繞組的優點是繞組端接部分縮短，導線用量減少，繞組線圈電阻降低，銅耗減少，效率提高，成本降低，製造週期縮短。但是集中繞組也帶來一定的缺點，主要是電機的繞組因數減小，定子磁動勢中諧波含量增加及定子齒、槽對磁場分佈的影響增大，使電機的脈動轉矩增大。

分佈繞組

分佈繞組

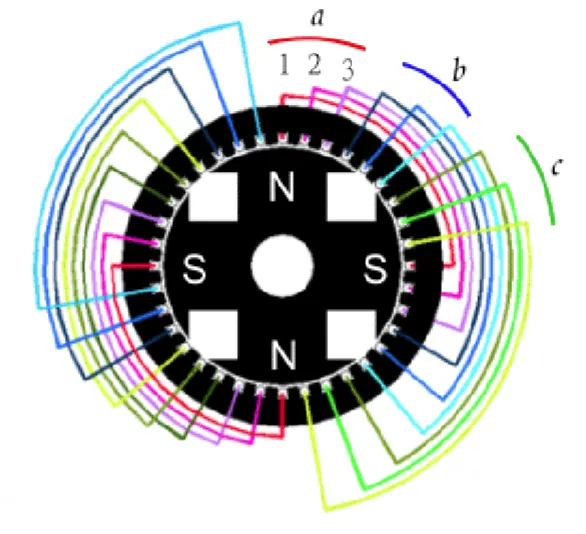
圖一、分佈繞組

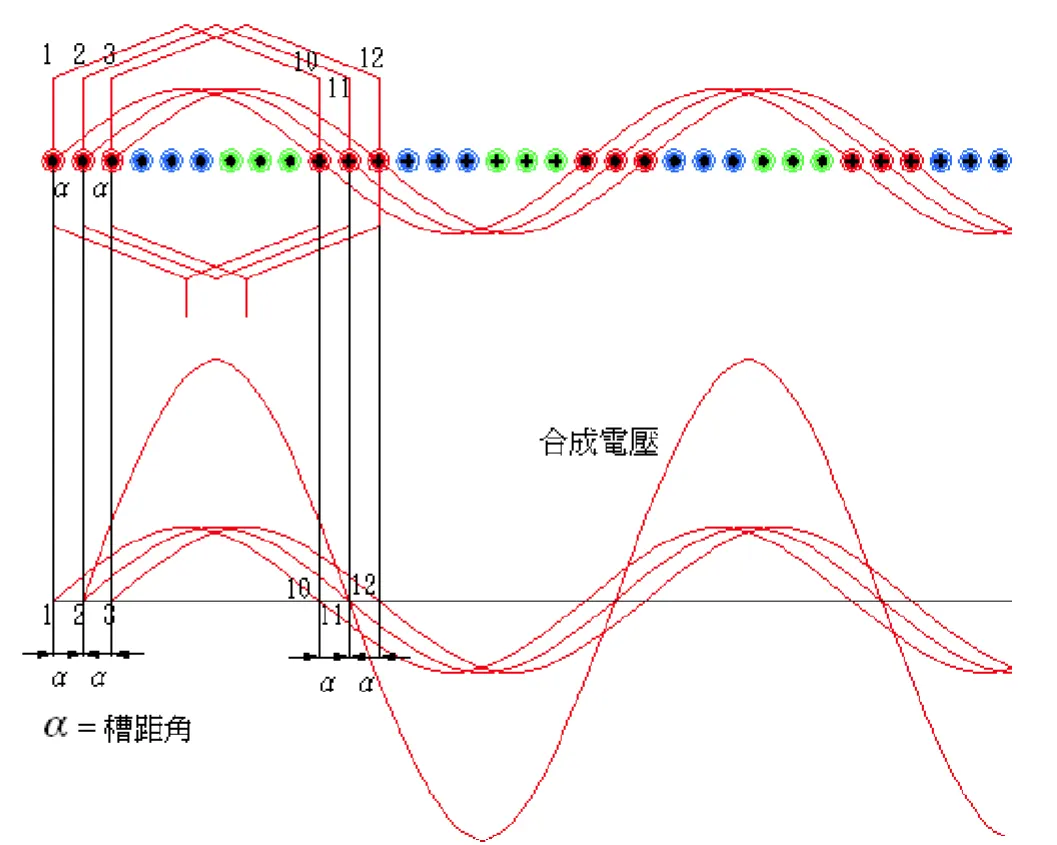
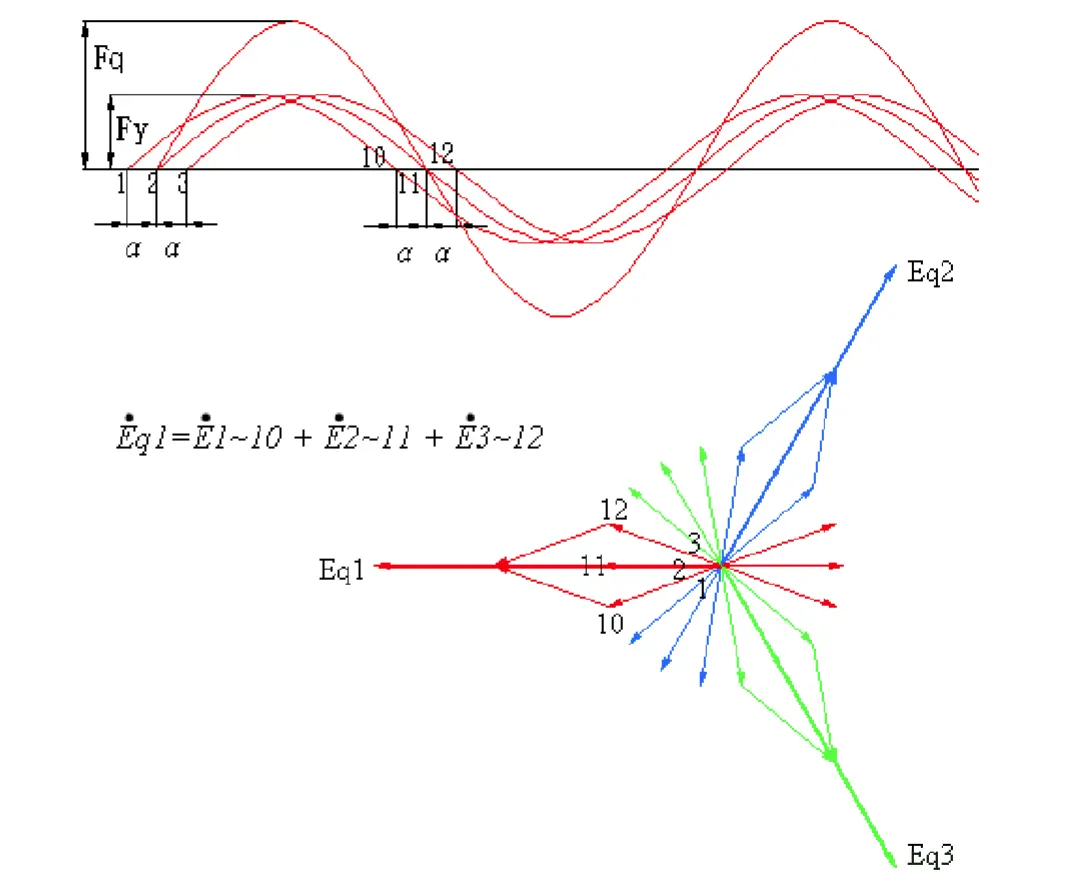
圖一、將每相繞組分散於三個定子槽內(1、2、3)且各組繞線相互串接，以a相為例其電壓合成為圖二中Fq，而各定子槽的線電壓為Fy，1、2、3組繞線在空間上各差一槽距角。

合成電壓

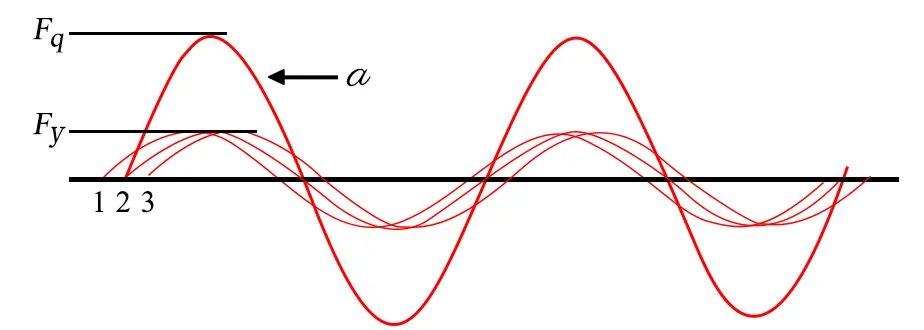
圖二、合成電壓

將一相的線圈分成q個等份且分別放置於同一相的q個定子槽內。設三相發電機定子槽數為N個，轉子極數為P極，則q= (N/p)/3。例：定子槽數為36槽轉子為4極q=(36/4)/3=3 即每相為三個槽(如前圖一)。在每槽線圈的兩端互相串接所合成的基本波仍為正弦波，由於各槽間相距一槽距角(上例為20°)使合成後的電壓小於分佈於各槽線圈的總合Fq < Fy1+Fy2+Fy3。

槽距角a：兩個定子槽之間的電氣角度。 a= 180°/(定子槽數N/轉子極數)

分佈係數： K q = 每相分佈繞組電壓 每相集中繞組電壓 = F q F y 1 + F y 2 + F y 3 Kq = \dfrac{每相分佈繞組電壓}{每相集中繞組電壓} = \dfrac{{Fq}}{Fy1+Fy2+Fy3}

分佈繞組的缺點為端部分太長、導線用量多、繞組線圈電阻高、銅耗大、效率降低、成本提高、製造複雜。 但其能被接受且廣為運用的主要優點：定子磁動勢中的諧波含量減少與定子齒、槽對磁場分佈的影響減小，使電機的脈動電壓幅度減小。

分佈繞組佈線方式一

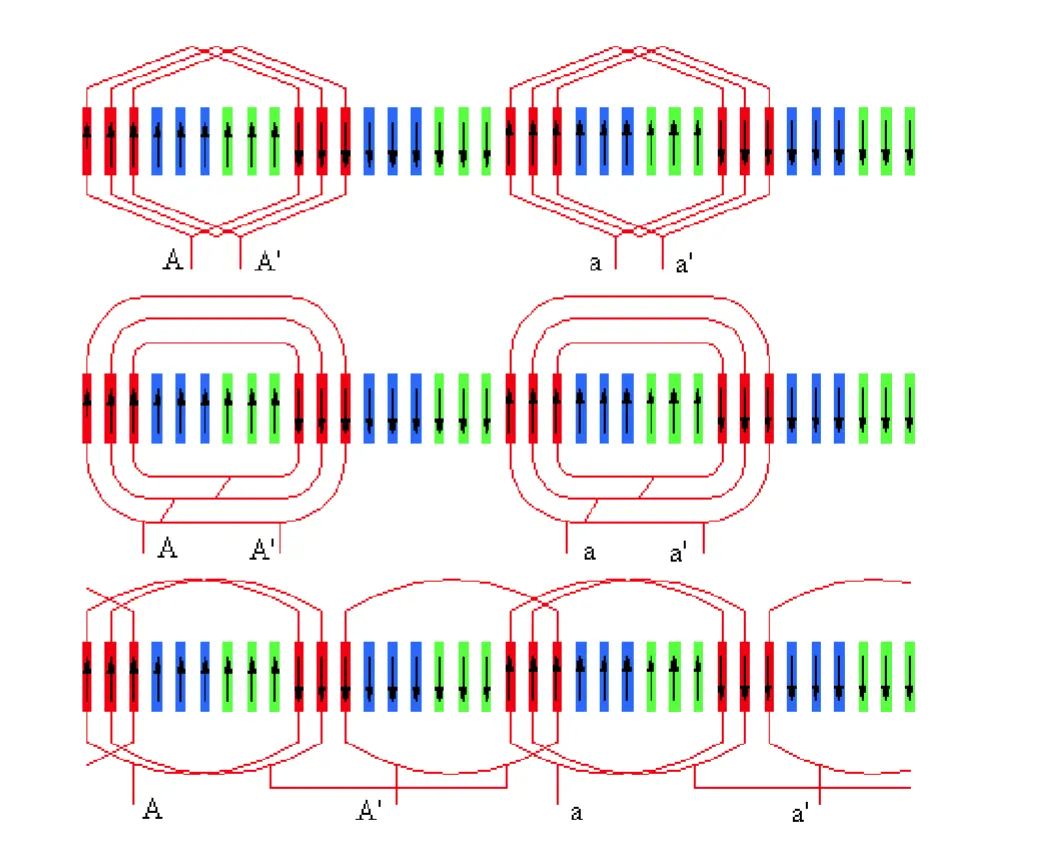
圖三、分佈繞組佈線方式(一)

分佈繞組佈線方式二

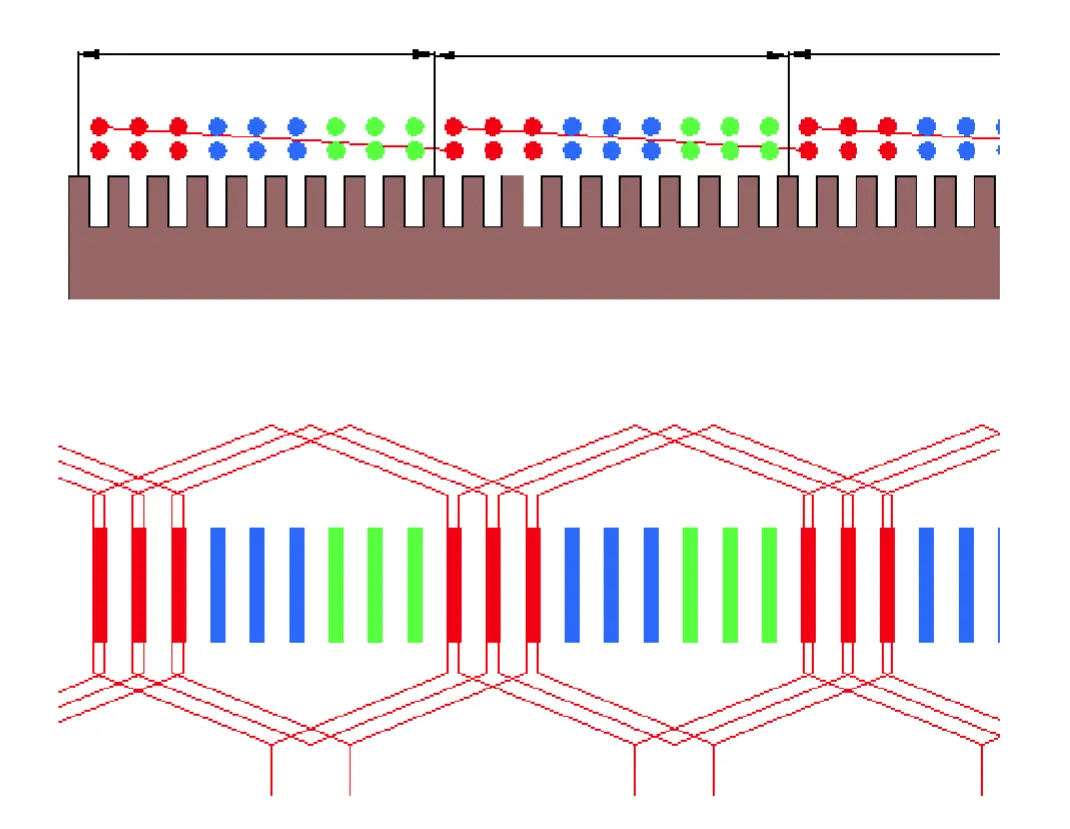
圖四、分佈繞組佈線方式(二)

電壓向量合成

圖五、電壓向量合成

雙層繞組結構一

雙層繞組結構一

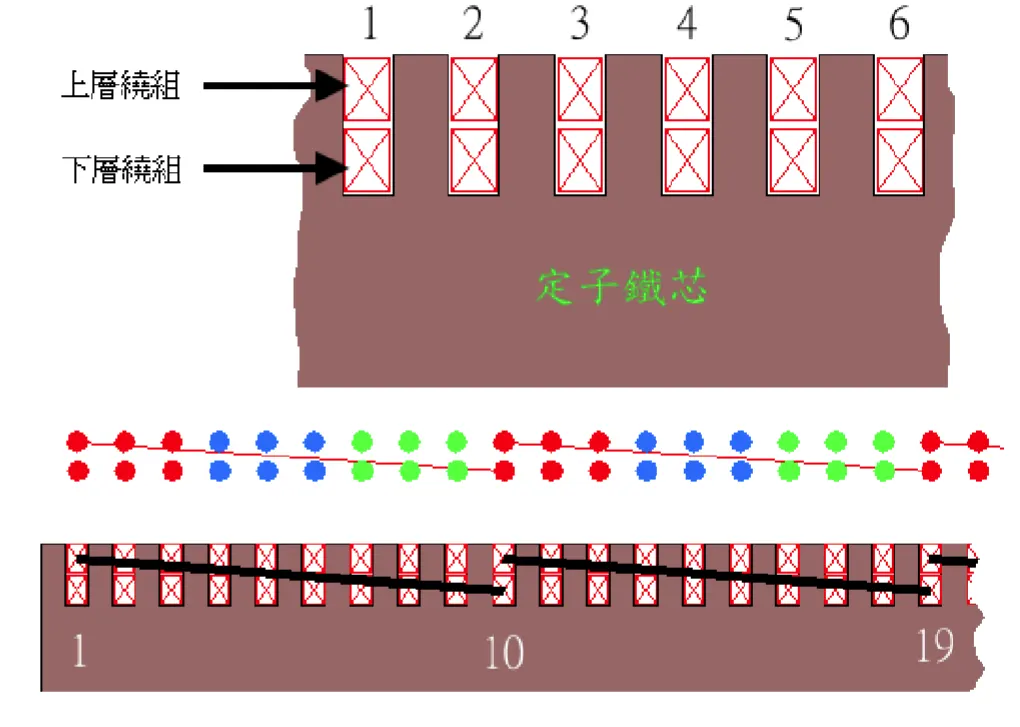
一般雙層繞組方式(36槽)為：第一槽上層與第十槽下層為一繞組，第二槽上層與第十一槽下層為一繞組，第三槽上層與第十二槽下層為一繞組... 第十槽上層與第十九槽下層為一繞組...依此類推。（如圖）

雙層繞組結構二

雙層繞組結構二

節距定義

節距定義
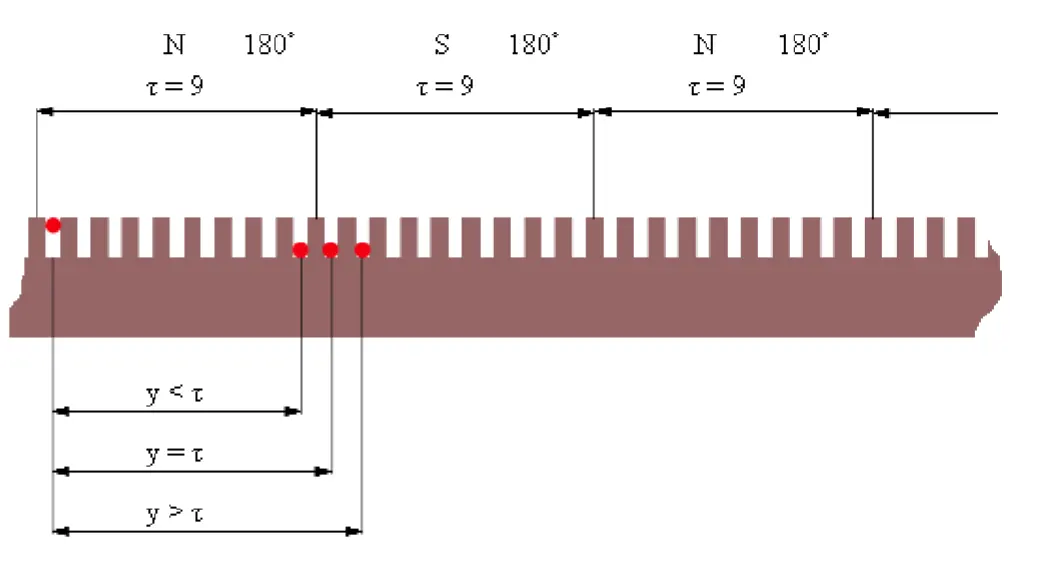
  • 線圈節距y：一個線圈兩個有效邊之間所跨過的槽數稱為線圈的節距。
  • 短節距：當線圈跨距小於極距τ 即y < τ
  • 整節距：當線圈跨距等於極距τ 即y = τ
  • 長節距：當線圈跨距大於極距τ 即y > τ

短節距繞組一

短節距繞組一

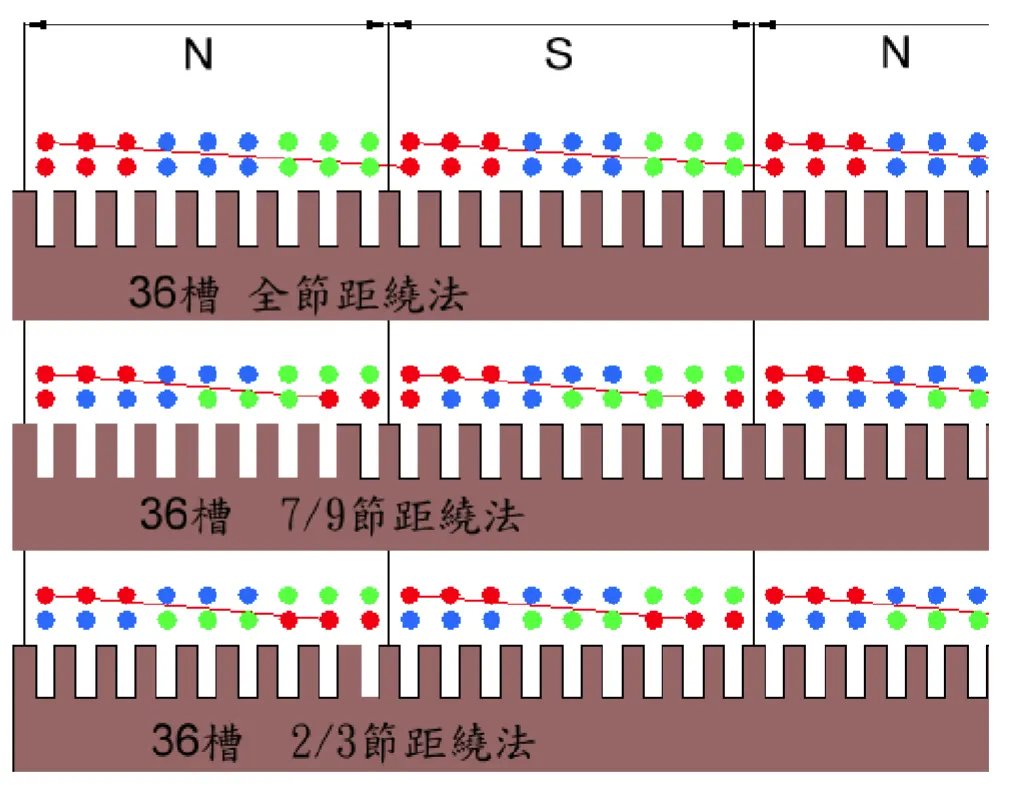
雙層全(短)節距繞組(一)

短節距繞組二

短節距繞組二

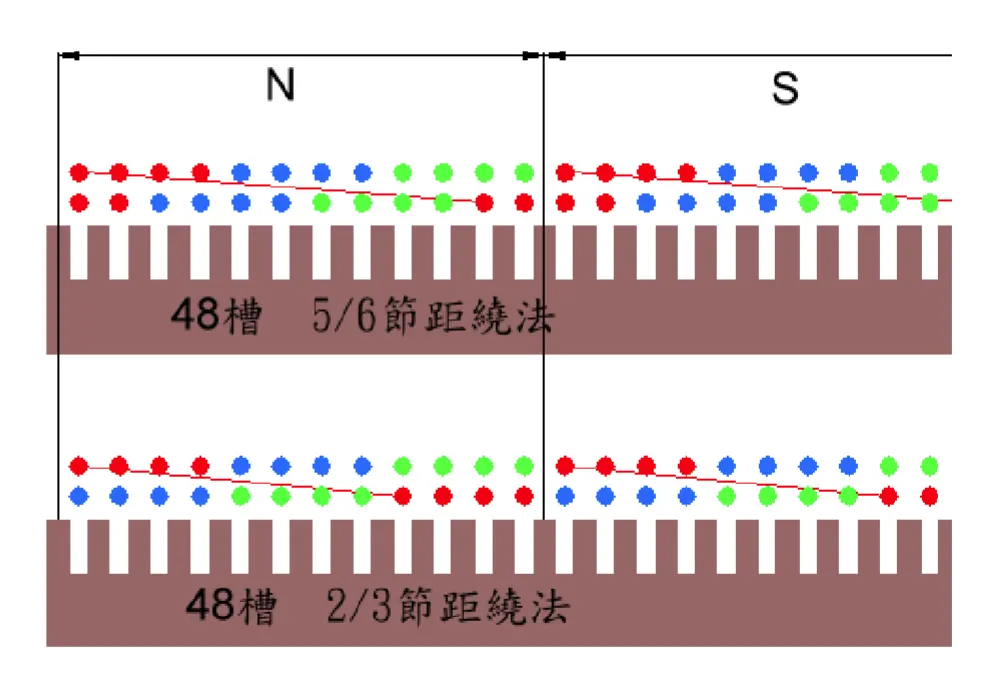
雙層全(短)節距繞組(二)

雙層短距分析一

雙層短節距繞組的磁勢
  • 在分析磁場分散式時，雙層整距繞組可以等效為兩個整距單層繞組。
  • 兩個等效單層繞組在空間分佈上錯開一定的角度，這個角度等於短距角。
  • 雙層短距繞組的磁勢等於錯開一個短距角的兩個單層繞組的磁勢在空間疊加。
  • 雙層短距繞組的磁勢為： F p 1 = 2 F q 1 cos ⁡ β 2 = 2 F q 1 k y 1 = 0.9 I y ( 2 q N y ) k q 1 k y 1 F_{p1} = 2F_{q1}{\cos}\dfrac{\beta}{2} = 2F_{q1}k_{y1} = 0.9I_y (2qN_y) k_{q1}k_{y1}
  • 繞組的短距係數： K y 1 = 短距繞組基波磁勢幅值 整距繞組基波磁勢幅值 = 2 F q 1 cos ⁡ β 2 2 F q 1 = cos ⁡ β 2 K_{y1} = \dfrac{短距繞組基波磁勢幅值}{整距繞組基波磁勢幅值} = \cfrac{2F_{q1}{\cos}\dfrac{\beta}{2}}{2F_{q1}} = {\cos}\dfrac{\beta}{2}

雙層短距分析二

雙層短距分析

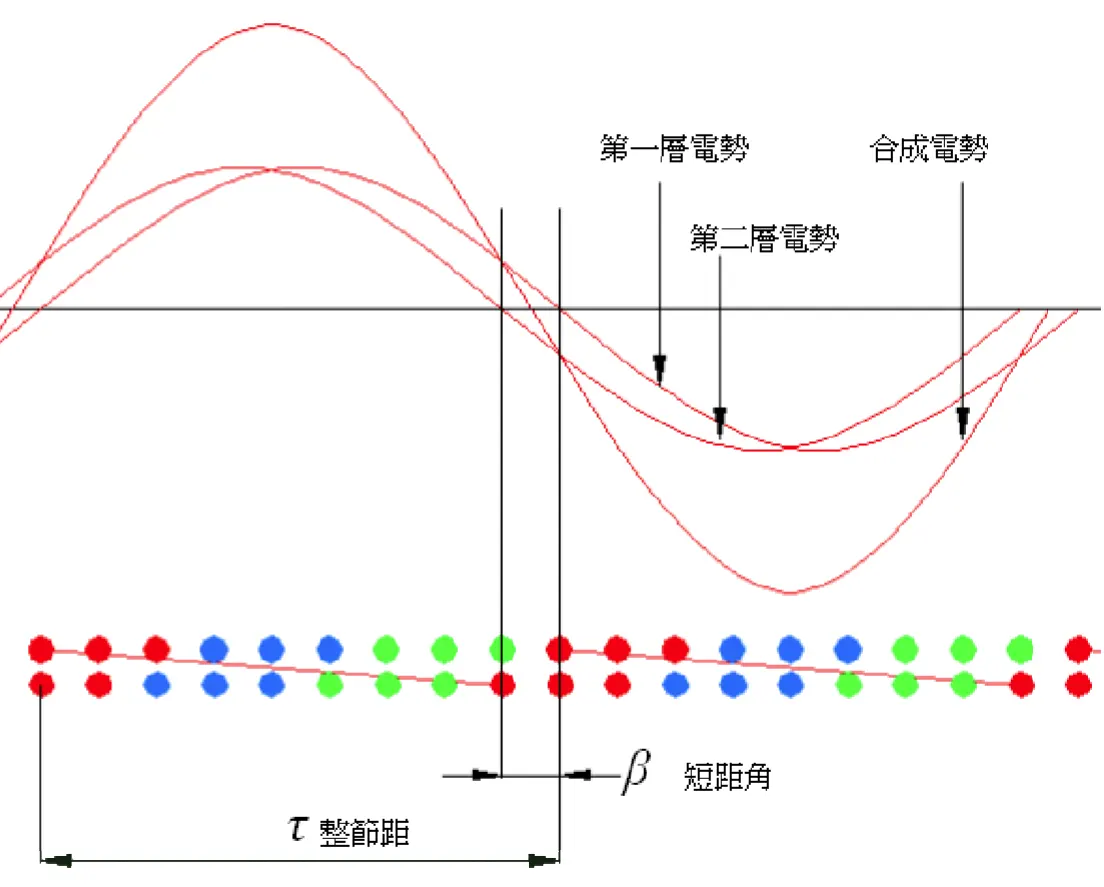
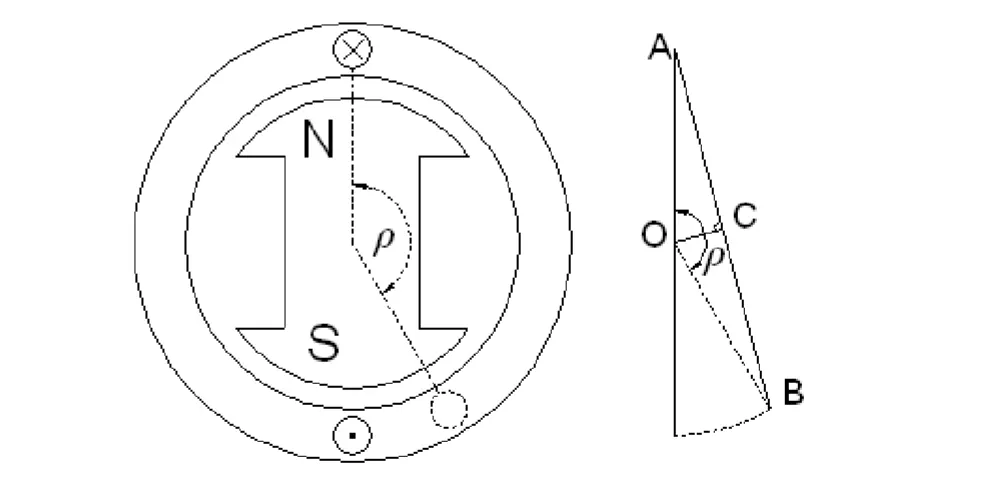
節距因數

節距因數Kp = 短節距感應電勢 全節距感應電勢    K p = A B ‾ 2 O A ‾ = A C ‾ O A ‾ = sin ⁡ ρ 2 \dfrac{短節距感應電勢}{全節距感應電勢}  Kp = \dfrac{\overline{AB}}{2\overline{OA}} =\dfrac{\overline{AC}}{\overline{OA}} = {\sin}\dfrac{\rho}{2}

ρ = 線圈分數跨距

節距因數

分佈因數

交流電機電樞繞組實際上採用分佈繞法即短節距繞法，以提高鐵心利用率及改善波型。
  • 感應電壓每項有效值： E α = 4.44 K w f N φ E{\alpha} = 4.44KwfN{\varphi}
  • 繞組因數 Kw= Kd × Kp
  • 分佈因數Kd
  • 節距因數Kp
  • ψ \psi ：每極磁通量wb
  • N：每相匝數
  • 每槽繞組感應電壓相同，相位差r°
分佈因數： K d = 分佈繞組電壓 集中繞組電壓 = sin ⁡ n γ 2 n    sin ⁡ γ 2 Kd = \dfrac{分佈繞組電壓}{集中繞組電壓} = \cfrac{\sin\dfrac{n\gamma}{2}}{n  \sin\dfrac{\gamma}{2}}
n：每相每極之槽數r：每槽電機角　

諧波與節距

諧波含量與線圈跨距
  • 若欲消除三次諧波電壓，則線圈跨距應如下：
  • 對基本波而言每槽電機角為r°，繞組跨距為ρ π(電角)
  • 對三次諧波而言每槽電機角為3r°，繞組跨距為3ρ π(電角)
  • 基本波電壓為 E a 1 = 4.44 K d 1    K p 1    f N φ E_a1 = 4.44Kd1  Kp1  fN{\varphi}
  • 三次諧波電壓為 E a 3 = 4.44 K d 3    K p 3    f N φ E_a3 = 4.44Kd3  Kp3  fN{\varphi}
若Kp3=0，則Ea3 = 0 即三次諧波電壓為零。
∴    K p 3 = sin ⁡ ( 3 ρ ) 2 = 0 \therefore  Kp3 = {\sin}\dfrac{(3{\rho})}{2} = 0
ρ = 2 3 π = = 120 ° \dfrac{2}{3} {\pi} = =120° (採2/3節距)

結論

分佈繞法之優點

  • ★ 提高鐵心利用率
  • ★ 散熱易，可提高繞組之載流能力
  • ★ 雖然感應電壓減少，但可使電壓波形趨近正弦波

短節距之優點

  • ★ 節省材料
  • ★ 改善波形

輸出端結線一

輸出端結線一

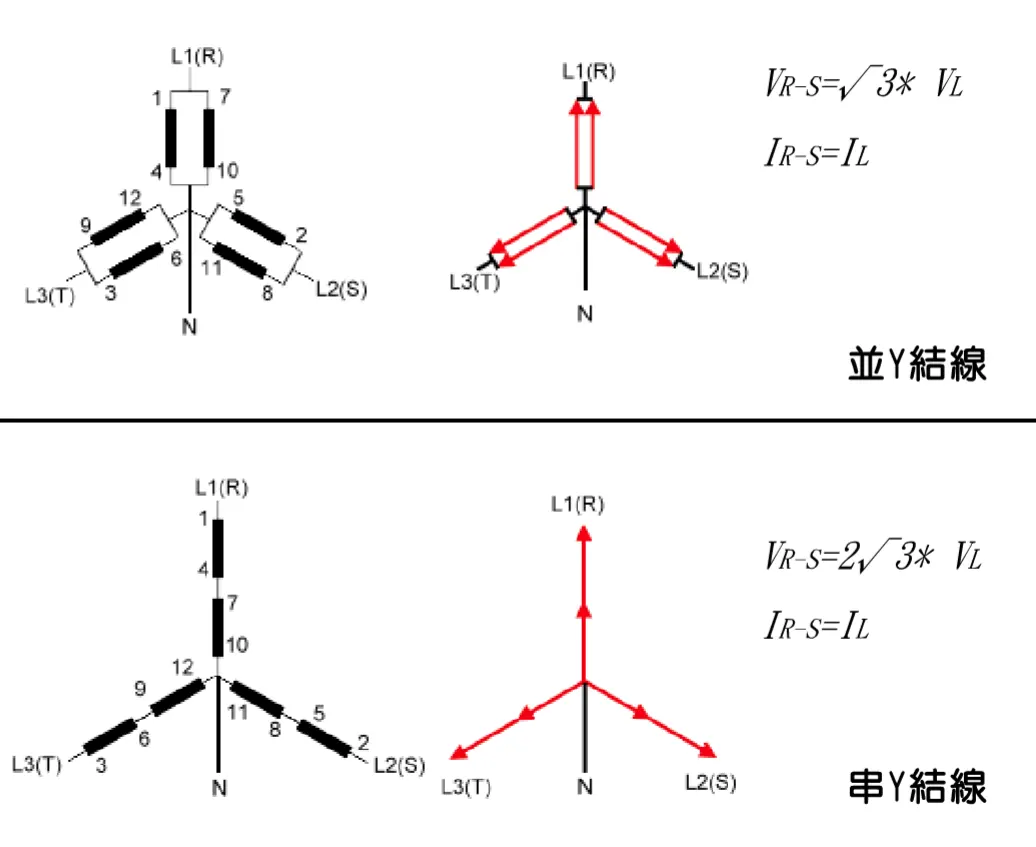
輸出端結線二

輸出端結線二

輸出端結線三

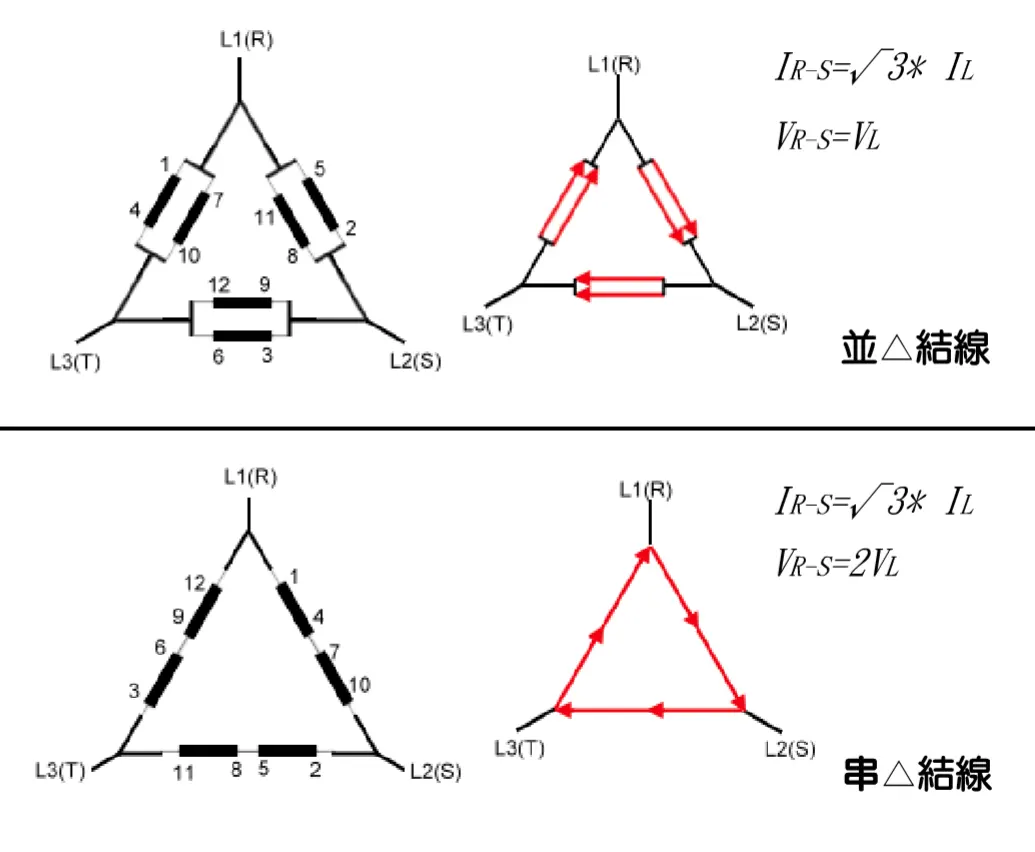
輸出端結線三