發電機定子繞組(二)

雙層繞組結構一

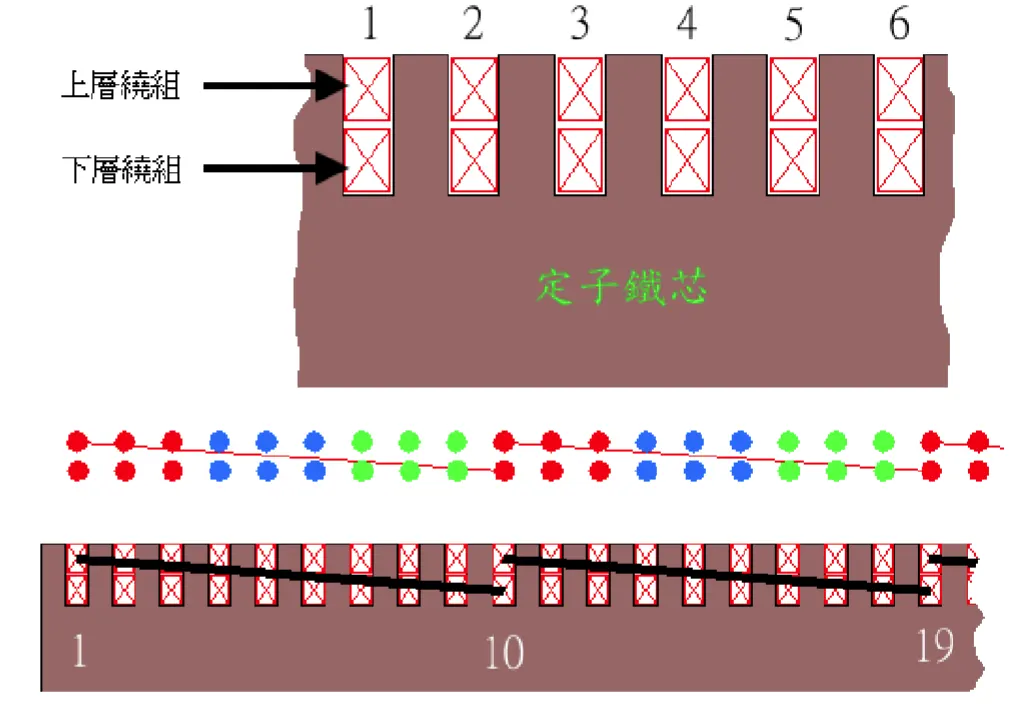
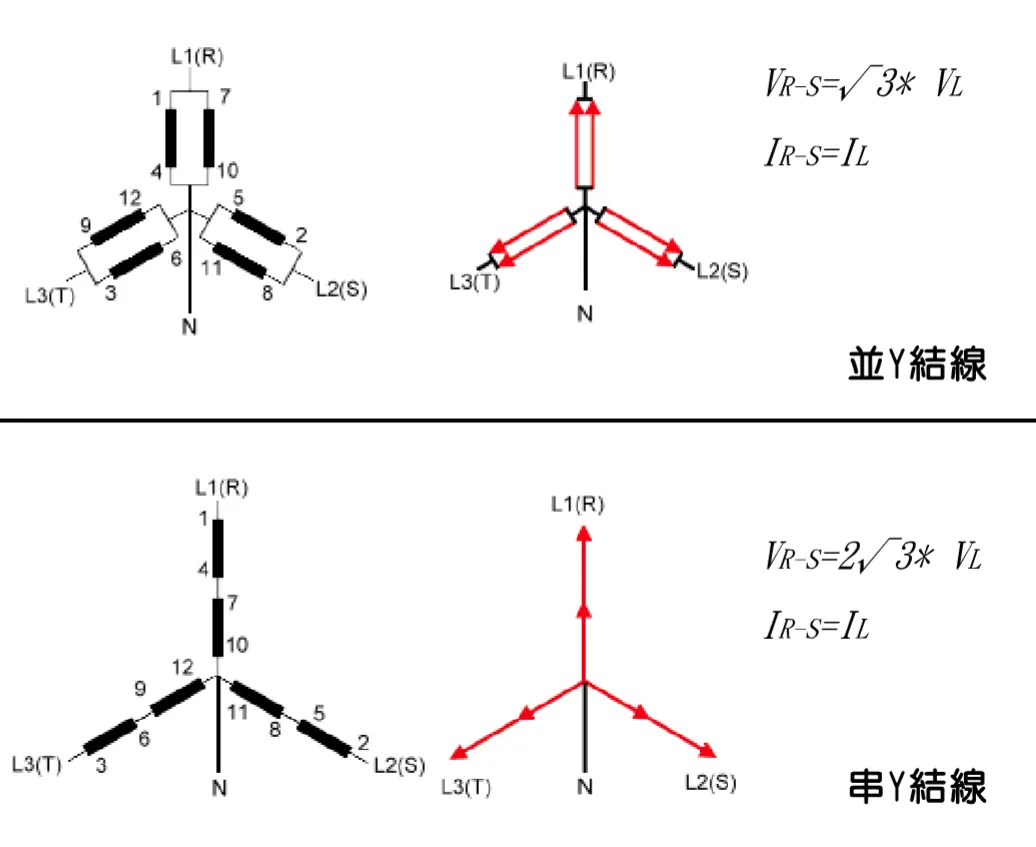
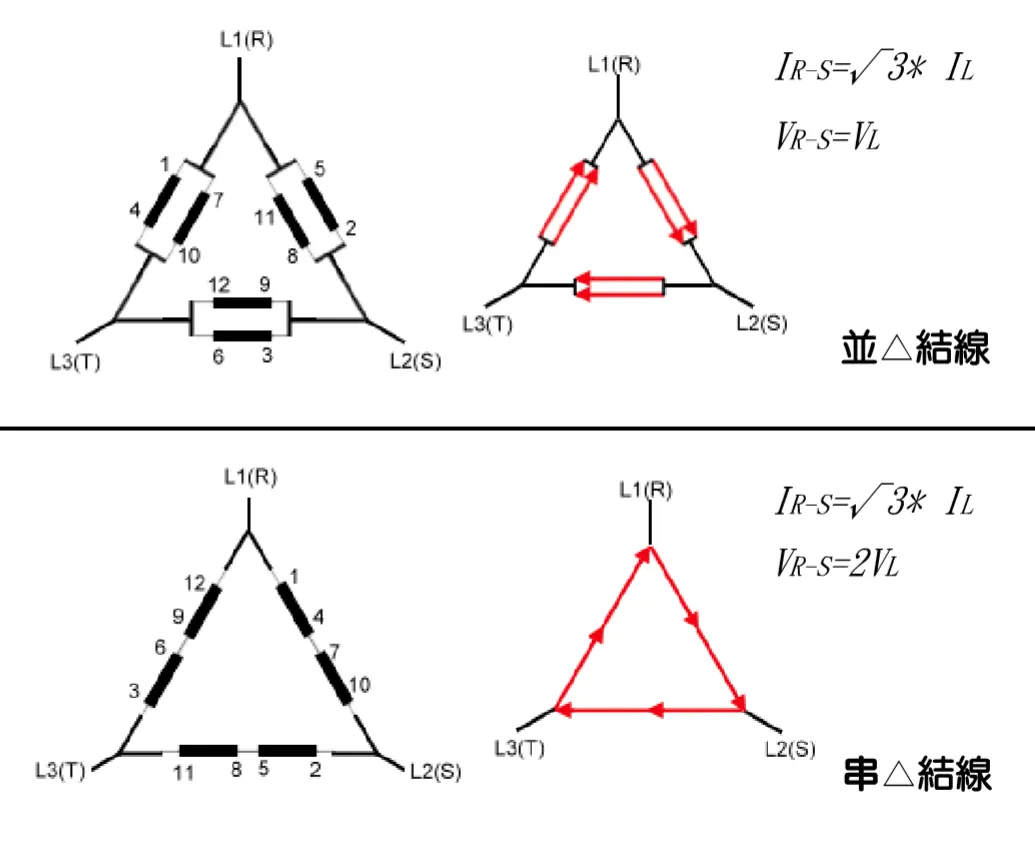
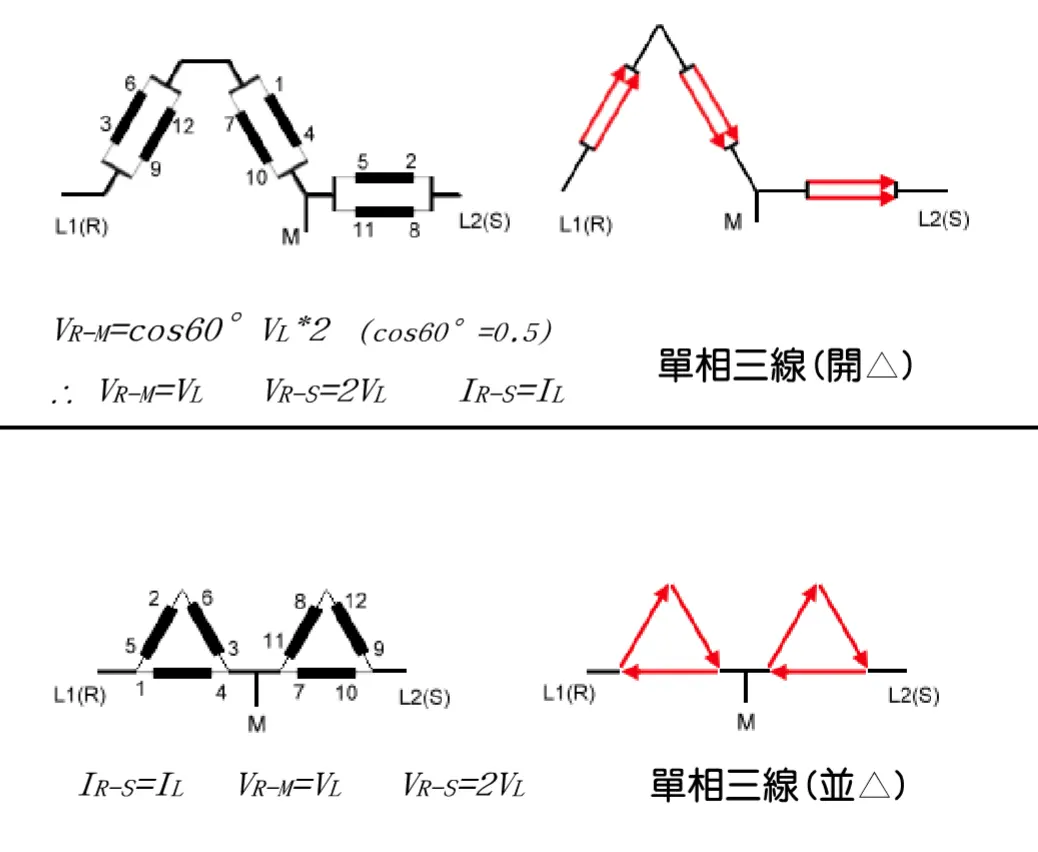
一般雙層繞組方式(36槽)為：第一槽上層與第十槽下層為一繞組，第二槽上層與第十一槽下層為一繞組，第三槽上層與第十二槽下層為一繞組... 第十槽上層與第十九槽下層為一繞組...依此類推。（如圖）

雙層繞組結構二

節距定義

線圈節距y：一個線圈兩個有效邊之間所跨過的槽數稱為線圈的節距。
短節距：當線圈跨距小於極距τ 即y < τ
整節距：當線圈跨距等於極距τ 即y = τ
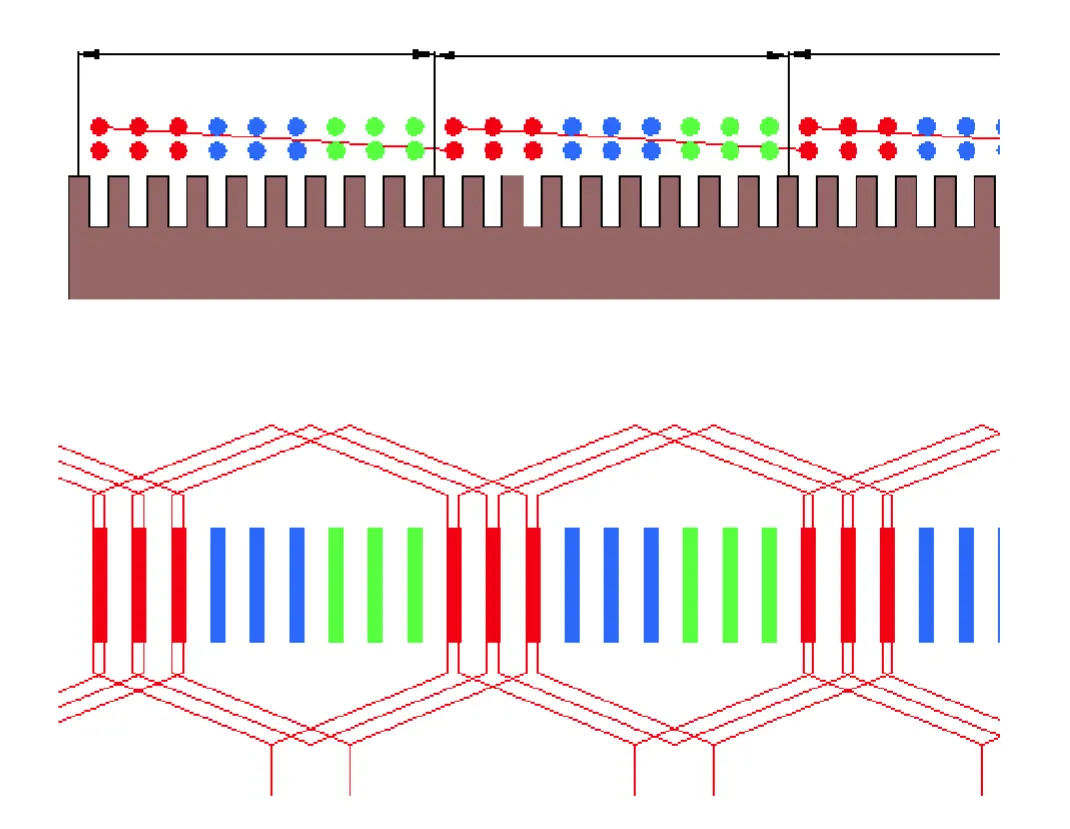
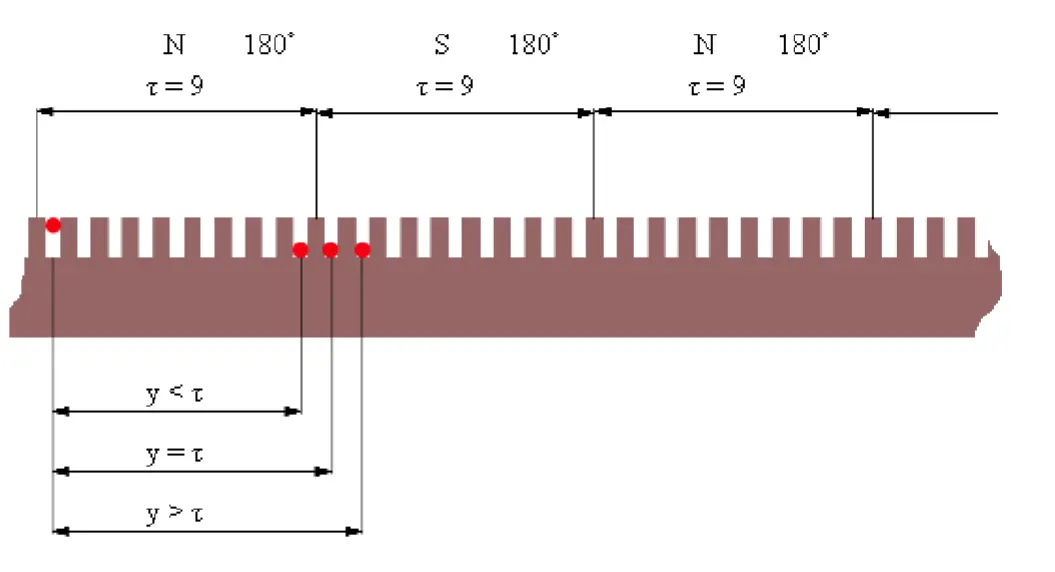
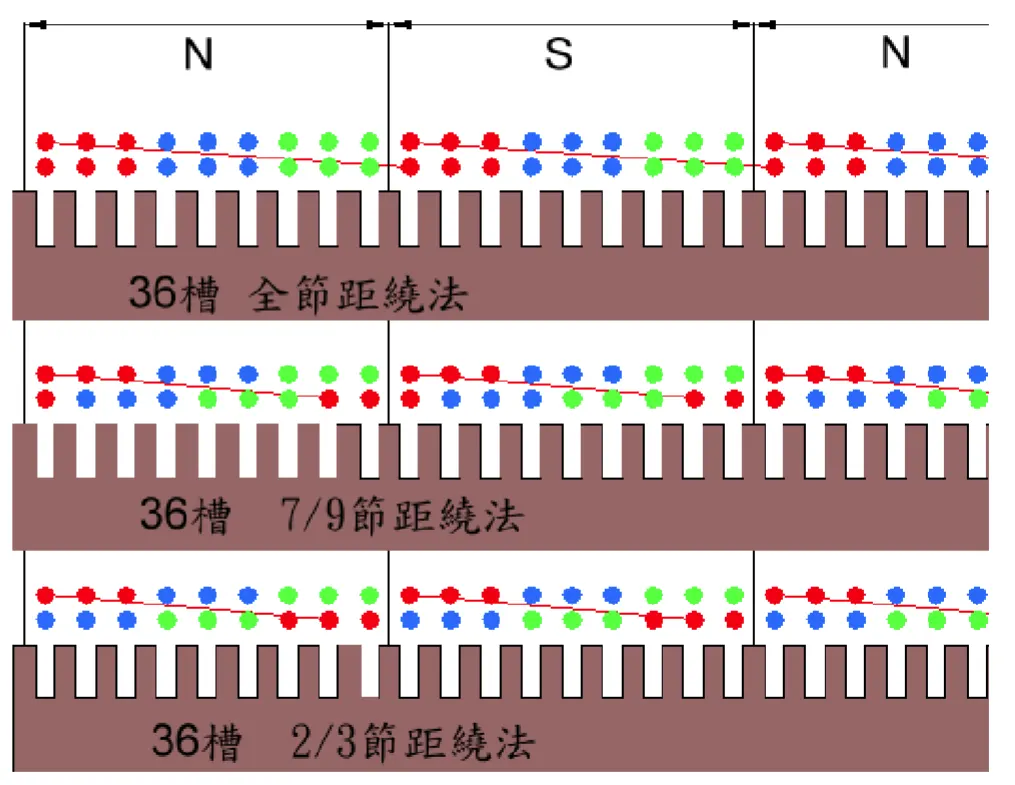
長節距：當線圈跨距大於極距τ 即y > τ

短節距繞組一

雙層全(短)節距繞組(一)

短節距繞組二

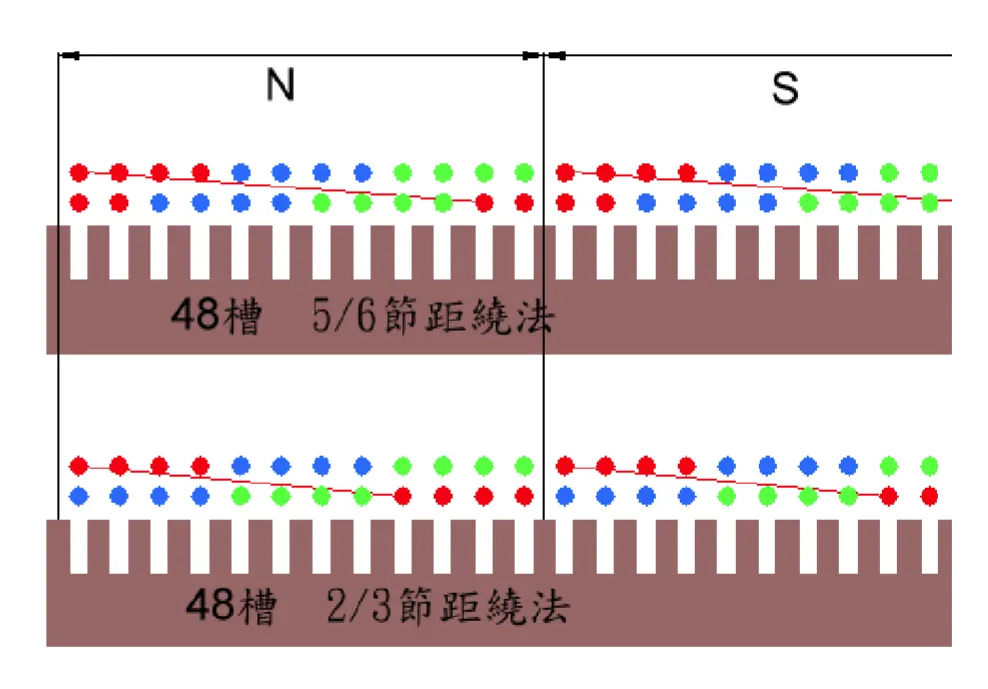
雙層全(短)節距繞組(二)

雙層短距分析一

雙層短節距繞組的磁勢

在分析磁場分散式時，雙層整距繞組可以等效為兩個整距單層繞組。
兩個等效單層繞組在空間分佈上錯開一定的角度，這個角度等於短距角。
雙層短距繞組的磁勢等於錯開一個短距角的兩個單層繞組的磁勢在空間疊加。
雙層短距繞組的磁勢為：\( F_{p1} = 2F_{q1}{\cos}\dfrac{\beta}{2} = 2F_{q1}k_{y1} = 0.9I_y (2qN_y) k_{q1}k_{y1} \)
繞組的短距係數：\( K_{y1} = \dfrac{短距繞組基波磁勢幅值}{整距繞組基波磁勢幅值} = \cfrac{2F_{q1}{\cos}\dfrac{\beta}{2}}{2F_{q1}} = {\cos}\dfrac{\beta}{2} \)

雙層短距分析二

節距因數

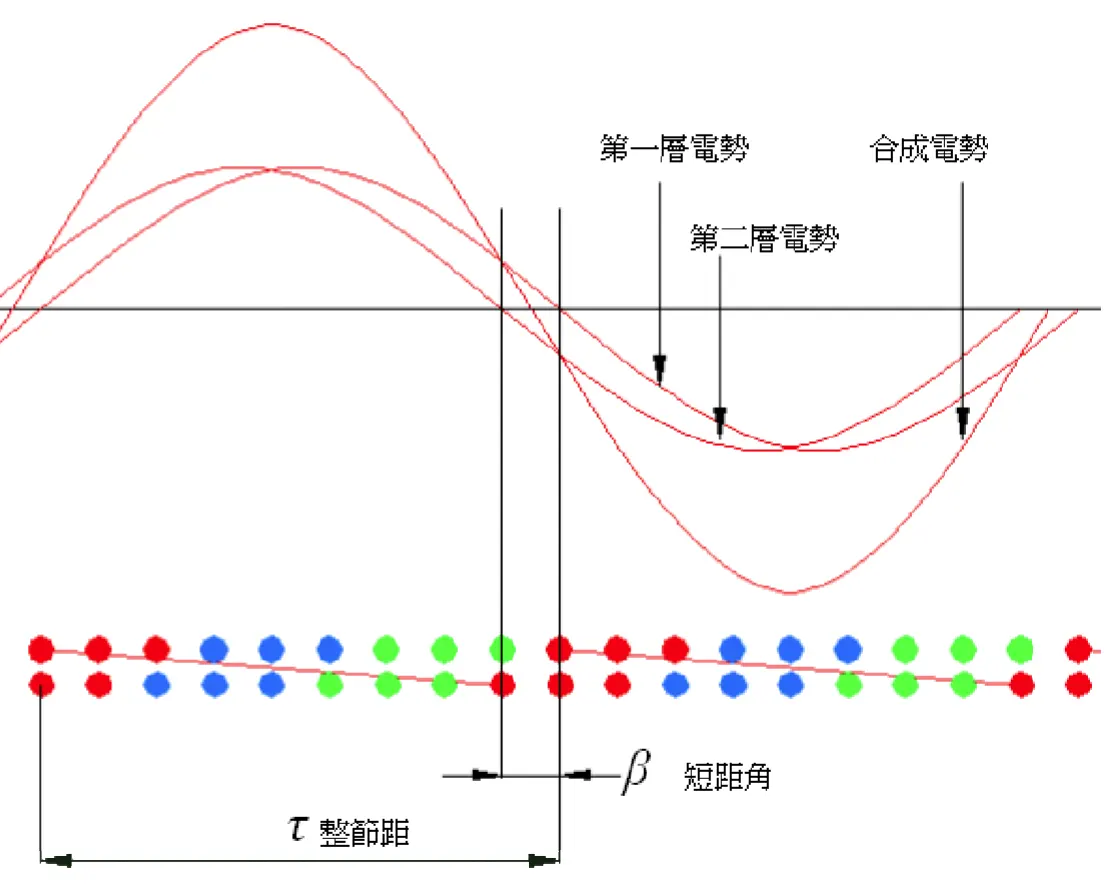
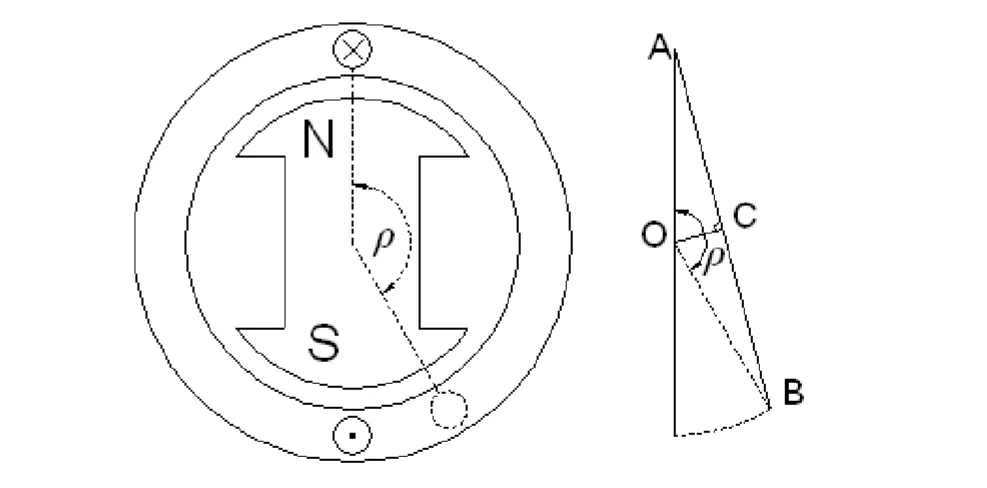
節距因數Kp = \( \dfrac{短節距感應電勢}{全節距感應電勢} Kp = \dfrac{\overline{AB}}{2\overline{OA}} =\dfrac{\overline{AC}}{\overline{OA}} = {\sin}\dfrac{\rho}{2} \)

ρ = 線圈分數跨距

分佈因數

交流電機電樞繞組實際上採用分佈繞法即短節距繞法，以提高鐵心利用率及改善波型。

感應電壓每項有效值：\( E{\alpha} = 4.44KwfN{\varphi} \)
繞組因數 Kw= Kd × Kp
分佈因數Kd
節距因數Kp
\(\psi\)：每極磁通量wb
N：每相匝數
每槽繞組感應電壓相同，相位差r°

分佈因數：\( Kd = \dfrac{分佈繞組電壓}{集中繞組電壓} = \cfrac{\sin\dfrac{n\gamma}{2}}{n \sin\dfrac{\gamma}{2}} \)

n：每相每極之槽數r：每槽電機角　

諧波與節距

諧波含量與線圈跨距

若欲消除三次諧波電壓，則線圈跨距應如下：
對基本波而言每槽電機角為r°，繞組跨距為ρ π(電角)
對三次諧波而言每槽電機角為3r°，繞組跨距為3ρ π(電角)
基本波電壓為 \( E_a1 = 4.44Kd1 Kp1 fN{\varphi} \)
三次諧波電壓為 \(E_a3 = 4.44Kd3 Kp3 fN{\varphi} \)

若Kp3=0，則Ea3 = 0 即三次諧波電壓為零。

\( \therefore Kp3 = {\sin}\dfrac{(3{\rho})}{2} = 0 \)

ρ = \( \dfrac{2}{3} {\pi} = =120° \) (採2/3節距)

結論

分佈繞法之優點

★ 提高鐵心利用率
★ 散熱易，可提高繞組之載流能力
★ 雖然感應電壓減少，但可使電壓波形趨近正弦波

短節距之優點

★ 節省材料
★ 改善波形